Statistics For Programmers - Bonus Content: Expressing a Taylor Polynomial in Code

A Taylor polynomial is generally used when approximating functions. They are especially useful when the true or exact form of the function is complex or difficult to work with.

By expressing a function as a Taylor series, it's possible to simplify calculations and gain insights into its behavior, particularly around the point where the series is centered. Expressing this as code is pretty interesting when broken down into its components. Let's take an example to see this in action:

\[ P_n(x) = \sum_{n=0}^\infty \frac{f^{(n)}a}{n!} \times (x - a)^n \]

Where:

• \( P_n(x) \) is the nth Taylor polynomial centered at a.
• \( a \) is the point at which the polynomial is centered.
• \( f^{(n)}a \) is the nth derivative of f evaluated at a.

Taking stock of what we have, we need to define the function \( f(x) \), the value of \( a \), and the value of \( n \). We can assume our function to be \( f(x) = 3x - 2x^3\), \(a=-3\) and \(n=3\). We can begin defining functions.

First we need to define a factorial function^[1]. This can be expressed as a simple recursive function.

function factorial(n) {
  if (n === 0) return 1;
  return n * factorial(n - 1);
}

Next we need to define a function that calculates the nth derivative of f. Since we know the function ahead of time we can manually compute the derivatives^[2] for each value of n.

function nthDerivative(n, x) {
  // f(x) = 3x - 2x^3
  if (n === 0) {
    // We're just returning the function itself
    return 3 * x - 2 * Math.pow(x, 3);
  } else if (n === 1) {
    // To calculate the first derivative we need to use the power rule
    // taking the parts of the function separately
    // 3x is a constant multiplied by x with no exponent so the derivative is 3
    // -2x^3 is a constant multiplied by x raised to the power of 3
    // so we subtract 1 from the exponent and multiply by the constant to get -6x^2
    return 3 - 6 * Math.pow(x, 2);
  } else if (n === 2) {
    // To calculate the second derivative we need to use the power rule again
    // 3 is a constant so the derivative is 0
    // -6x^2 is a constant multiplied by x raised to the power of 2
    // so we subtract 1 from the exponent and multiply by the constant to get -12x
    return -12 * x;
  } else if (n === 3) {
    // To calculate the third derivative we need to use the power rule again
    // 0 is a constant so the derivative is 0
    // -12x is a constant multiplied by x so we subtract 1
    // from the exponent and multiply by the constant to get -12
    return -12;
  }

  // Higher derivatives are 0
  return 0;
}

Finally we can define the function \( P_n(x) \). We'll need to define a function that calculates the sum of the series.

function sumSeries(n, f, a, x) {
  let sum = 0;
  for (let i = 0; i <= n; i++) {
    sum += (f(i, a) / factorial(i)) * Math.pow(x - a, i);
  }
  return sum;
}

Now we can plug in the values we know and solve for x.

const a = -3;
const n = 3;
const x = 2;
const result = sumSeries(n, nthDerivative, a, x);
console.log(result);

// -10

While we can now compute the value of the function for a given value of x, it gets a lot more interesting when we plot the values for a range of x values.

const values = [];
for (let n = 0, n <= 3; n++) {
  for (let x = -3; x <= 3; x++) {
    values.push(sumSeries(n, nthDerivative, a, x));
  }
}

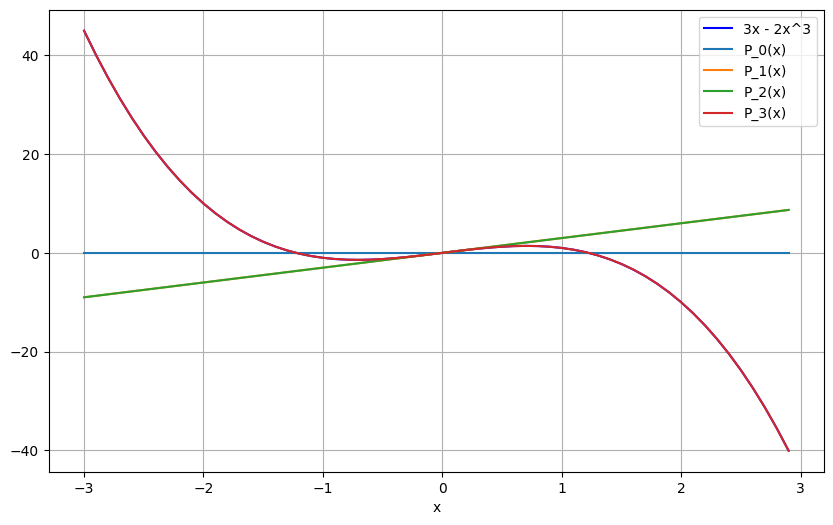
Plotted against the original function \( f(x) = 3x - 2x^3 \) we get the following graph you can see that the function approximates the original function for increasing values of n (P_3(X) overlaps the function).